回路図でのスイッチ
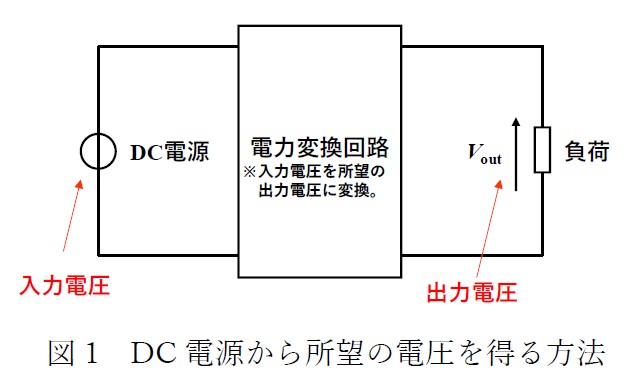 それではスイッチとダイオードを使って、図1 の通り、DC 電源から入力された直流電圧を所望の直流電圧(出力電圧)に変換する回路を見ていきましょう。
それではスイッチとダイオードを使って、図1 の通り、DC 電源から入力された直流電圧を所望の直流電圧(出力電圧)に変換する回路を見ていきましょう。
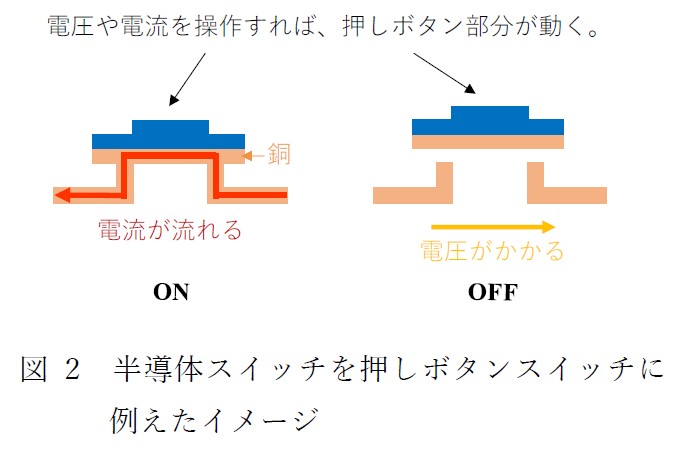
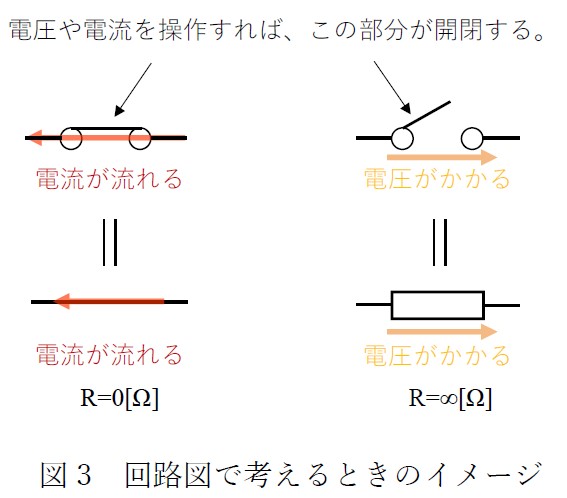
過去の記事ではスイッチを図2 の通りに押しボタンスイッチに見立てて説明しました。今回からスイッチのON/OFF は理想的に図3 の通り表現し、スイッチがON の時は導線と同じで回路的にR=0、スイッチがOFF の時は回路的にR=∞(無限)になると仮定します。
 |
 |
ところで、スイッチをON させた場合をショートとか短絡、スイッチOFF させた場合をオープンとか開放と呼ぶこともあります。このような単語が説明ででてきたときは、そうなんだと頭の片隅に置いといてください。
電気回路のタブー
電気回路ではやってはいけないタブーがあります。そこで、スイッチ+受動素子の回路を理解する前に、まず電気回路でやってはいけないタブーを理解しましょう。
世の中には様々な回路がありますが(といっても使われている回路方式は限定的)、ほとんどの回路はこのタブーを避けています。早速、インダクタとスイッチを繋ぐ際のタブーを見てみます。
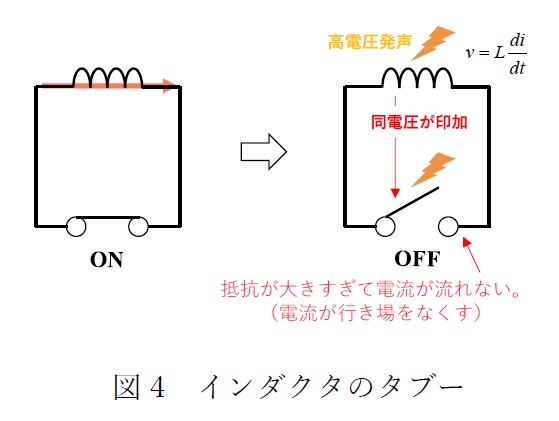 例えばですが、図4 の通り、インダクタにスイッチを介して電流が流れていて、スイッチを急にOFF した場合を考えてみます。R=∞[Ω]なので、電流が流れないですよね…
例えばですが、図4 の通り、インダクタにスイッチを介して電流が流れていて、スイッチを急にOFF した場合を考えてみます。R=∞[Ω]なので、電流が流れないですよね…
つまり、電流が行き場を無くします。抵抗が∞Ωなので電流が一瞬にして0 になります。電流が0 になるということはどういうことでしょうか?
インダクタの電流と電圧の関係Ldi/dt=v を思い出してください。電流が急に0になるということはdi/dt が負側の無限の値に近くなるということです。となると、キルヒホッフの法則からインダクタに印加される電圧と同等の電圧がスイッチに印加されます。つまり、無限大の電圧です…。これにより、スイッチが破壊されてしまいますので、電源ではこのような動作を避けなければいけません。しかしながら、完全には避けれないので、実際の電源では“サージ” という鋭くて大きな電圧がスイッチの両端電圧波形に表れてくるのです。
次にキャパシタとスイッチのタブーです。
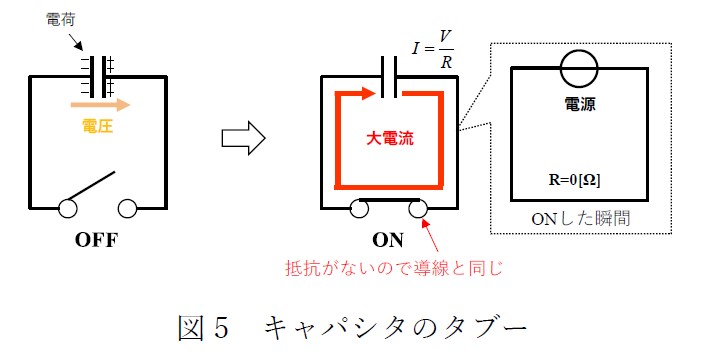 例として、図5 の状態を考えてみましょう。キャパシタにはある程度の電荷が蓄積されており、電圧が発生しています。この状態でスイッチをON させるとどうなりますか?スイッチをON させた瞬間を簡単な回路で書くと、DC 電源が短絡されている状態(R=0[Ω])と同じなので、I=V/R から無限大の電流がスイッチに流入し、スイッチの破損に繋がることが容易に想像できます。
例として、図5 の状態を考えてみましょう。キャパシタにはある程度の電荷が蓄積されており、電圧が発生しています。この状態でスイッチをON させるとどうなりますか?スイッチをON させた瞬間を簡単な回路で書くと、DC 電源が短絡されている状態(R=0[Ω])と同じなので、I=V/R から無限大の電流がスイッチに流入し、スイッチの破損に繋がることが容易に想像できます。
それでは、世の中の回路ってもしかして組み合わせに法則性がある?って疑問がわきますのよね。
答えは簡単でキャパシタの次はインダクタ、インダクタの次はキャパシタといった感じで、インダクタ、キャパシタ、インダクタ、キャパシタ…という構成になっています。
なぜなのか。昔のことを思い出してみてください。スイッチに大電圧がかかるのであれば、電圧の変化を嫌うキャパシタを挿入したら、電圧の変化を抑制できます。スイッチに大電流が流れるのであればインダクタを挿入したら、電流の変化を抑制できます。実際に電源回路はこれらのタブーが起こらないようにインダクタとキャパシタを組み合わせて構成されているのです。
もし機会があれば、さまざまな回路を確認してみてください。ほんとだっ!!って感じると思いますよ。
次に、過渡状態と定常状態です。どこかの記事で過渡現象をやりましたよね?
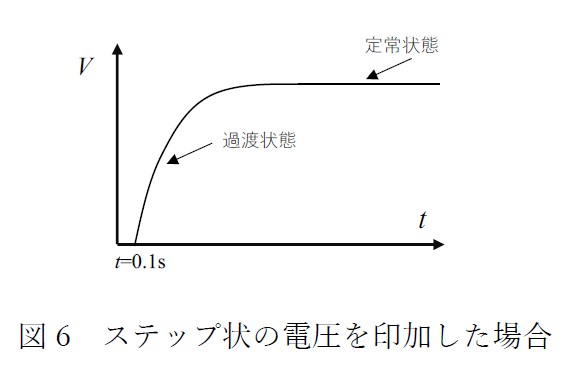 もちろんインダクタ、キャパシタ、ダイオードやスイッチで構成される電源回路もコンセントにプラグを挿した際に過渡状態が続いた後に定常状態となります。前回やったステップ状の電圧を印加した場合(図6)、過渡状態は電圧が一定になるまでの状態、あるいは電流が一定になるまでの状態と理解でき、定常状態は電圧と電流の値が一定になる状態だと何となく理解できます。スイッチのON/OFF にて動作する電源回路にも定常状態はあるのでしょうか?もちろん、あります。
もちろんインダクタ、キャパシタ、ダイオードやスイッチで構成される電源回路もコンセントにプラグを挿した際に過渡状態が続いた後に定常状態となります。前回やったステップ状の電圧を印加した場合(図6)、過渡状態は電圧が一定になるまでの状態、あるいは電流が一定になるまでの状態と理解でき、定常状態は電圧と電流の値が一定になる状態だと何となく理解できます。スイッチのON/OFF にて動作する電源回路にも定常状態はあるのでしょうか?もちろん、あります。
では何が定常状態となるのでしょうか?
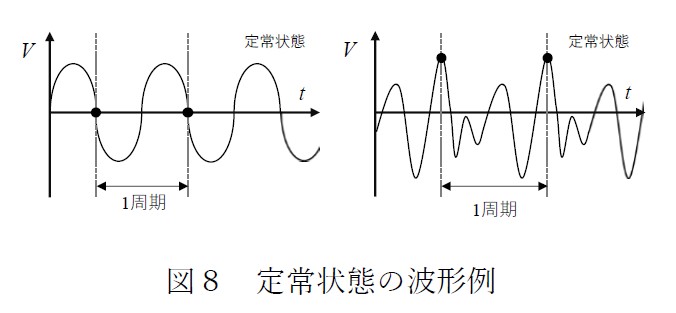
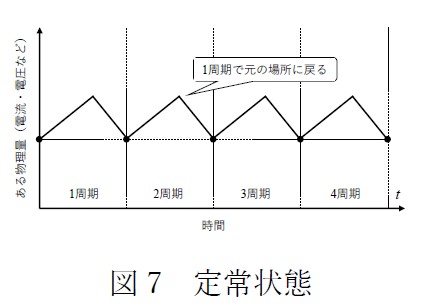 電源回路はではスイッチのON/OFF の周期や周波数をスイッチング周期やスイッチング周波数と呼びますが、このスイッチング周期の始まりと終わりでインダクタの電圧・電流やキャパシタの電圧・電流が同じ値となり、周期的に同じ動作になった状態を定常状態と呼んでいます。これは図7 と図8 の通りです。ここで定常状態になったときには以下のことが成り立ちます。
電源回路はではスイッチのON/OFF の周期や周波数をスイッチング周期やスイッチング周波数と呼びますが、このスイッチング周期の始まりと終わりでインダクタの電圧・電流やキャパシタの電圧・電流が同じ値となり、周期的に同じ動作になった状態を定常状態と呼んでいます。これは図7 と図8 の通りです。ここで定常状態になったときには以下のことが成り立ちます。
 |
 |
■図8 より
・インダクタ電流の増減は0(定常状態だから)。
・キャパシタ電圧の増減は0(定常状態だから)。
■図9 より
・1 周期におけるインダクタの電圧の面積の足し算は0 となる。
・1 周期におけるキャパシタの電流の面積の足し算は0 となる(図9)。
これは電源回路を考える上で非常に重要でこの状態を使って、入出力の数式が導出できます。
今回はここまで。次回はついに回路の動きを読み解いていきましょう。
参考・引用文献
[1] 今回はなし
注:2020/1に作成頂いた分です。






 :
: :
: