受動素子のイメージ
それでは今回は受動素子のイメージを掴みましょう。
まずは抵抗からです。抵抗のイメージを人の混雑状態で考えてみましょうか。
例えば、電流の流れは人の流れ、電流の大きさは人間の数に対応すると考えてください。
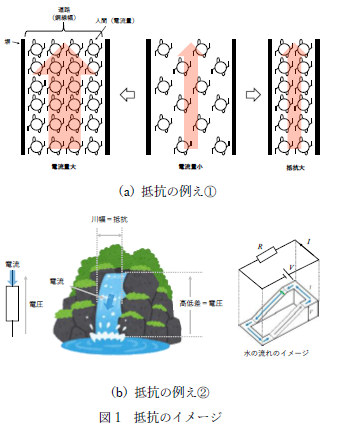 図 1(a)の真ん中(電流量小)を基準考えます。図 1 の通り、人間が塀と塀に囲まれている道路を下から上(矢印の方向)に移動しているとすると、真ん中のように人間の数に対して道幅が大きい場合、人間が少ないので人間同士あるいは塀人間が塀にぶつかったりしませんよね。一方で左の図の通り、人間が多い場合、人間同士や人間が塀にぶつかる可能性が大きくなります。ぶつかるとどうなるでしょうか?摩擦が生じて熱が発生しそうです ね。これを人間の数→電流の大きさ、道幅の広さ→抵 抗に置き換えると、抵抗に大きな電流を流すと明らかに熱が発生するとイメージできるでしょう。ところで、図 1 の右図は電流の大きさはそのままで道路の幅を小さく(抵抗値を大きく)した場合です。この場合も人間同士や塀にぶつかる可能性が大きくなるので、電流の大きさが同じであれば、発熱が大きくなると理解できます。次に電圧の概念を入れてみましょう。よくV=IR の関係は高低差のある水の流れにも例えられます。
図 1(a)の真ん中(電流量小)を基準考えます。図 1 の通り、人間が塀と塀に囲まれている道路を下から上(矢印の方向)に移動しているとすると、真ん中のように人間の数に対して道幅が大きい場合、人間が少ないので人間同士あるいは塀人間が塀にぶつかったりしませんよね。一方で左の図の通り、人間が多い場合、人間同士や人間が塀にぶつかる可能性が大きくなります。ぶつかるとどうなるでしょうか?摩擦が生じて熱が発生しそうです ね。これを人間の数→電流の大きさ、道幅の広さ→抵 抗に置き換えると、抵抗に大きな電流を流すと明らかに熱が発生するとイメージできるでしょう。ところで、図 1 の右図は電流の大きさはそのままで道路の幅を小さく(抵抗値を大きく)した場合です。この場合も人間同士や塀にぶつかる可能性が大きくなるので、電流の大きさが同じであれば、発熱が大きくなると理解できます。次に電圧の概念を入れてみましょう。よくV=IR の関係は高低差のある水の流れにも例えられます。
図 1(b)に示す通り、水の流れる川幅が広いほど水量が多く(抵抗が小さく電流量が多い)、狭いほど水量が少なく(抵抗が大きく電流量が少ない)なりそうなのが理解です。ここで高低差(電圧)を大きくすると、流れる水量(電流)が多くなり、小さくすると流れる水量(電流)が少なくなるので、電流値が増えます。 以上を要約しますと、抵抗の役割は ①電気エネルギーを熱エネルギーに変換する。 ②抵抗値によって電流をコントロール(制御)する。 と理解できるでしょう。
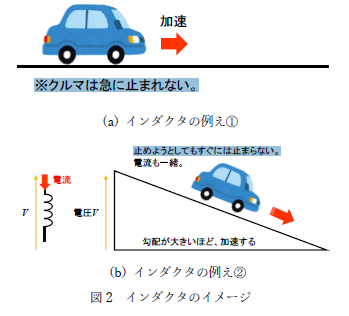 次にインダクタです。インダクタは前回の説明で、電流の変化を嫌うとお伝えしましたが、これをクルマの動きに例えてみます。
次にインダクタです。インダクタは前回の説明で、電流の変化を嫌うとお伝えしましたが、これをクルマの動きに例えてみます。
今度は図 2 の通り、クルマの動きを電流の動きと考えてみてください。クルマは一度加速して走り始めるとすぐに止まることはできず、慣性により走り続けようとしますよね。これをインダクタの電流の動きに対応させると、インダクタに流れる電流はクルマの動きと一緒ですぐに電流は止められず、徐々に 0 に向かっていくとうことになります。ここにさらに電圧の概念を加えると、図 2(b)の通り、坂道を下るクルマがしっくりくると思います。
坂道の高さを電圧の大きさとすると、高さが高いほど時間あたりの車の速度は上昇し、時間あたりの電流変化値が大きくなると理解できます。つまり、インダクタは電流の変化を嫌いますが、その一方で、インダクタの両端電圧(坂道の傾斜)は容易に変化できる素子となります。
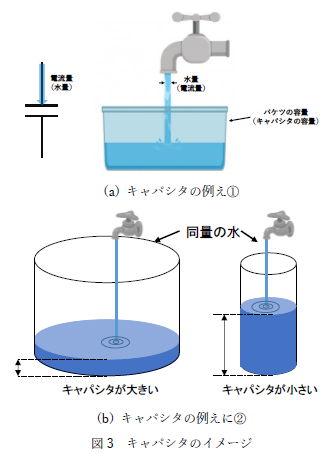
最後にキャパシタです。よくキャパシタは図 3 の通り、水とバケツで例えられます。キャパシタは電圧の変化を嫌いますが、この電圧の変化をバケツ内の水量の高さに例えてみましょう。図 3(a)の通り、蛇口の水がバケツに注がれていますが、水量の高さは急に変化することはなく、徐々に上昇していくことがわかります。また、この水量の上昇速度は注がれる水量あるいはバケツの大きさで変わることが図2(b)の通り、簡単に理解できます。これを電圧と電流に例えると電流量が少ないときは電圧があまり上昇せず、電流量が多いときは電圧がすぐに上昇してしまうことに対応しています。また蛇口から流れる水量は多くても少なくても簡単にバケツへ注げることがわかります。つまり、キャパシタは電圧の変化を嫌いますが、電流の出し入れは容易な素子となります。
受動素子の振る舞いpart2
では、実際にパワエレで使用される受動素子の動きを波形とともに確認しましょう。
パワエレでは受動素子に 0 からある値までの電圧を瞬時に印加することが多々あります。皆さまこの瞬時に電圧が印加される内容は大学講義で習ったのではないでしょうか。
それではこれまでの内容を基に、受動素子の動きを考えてみましょう。
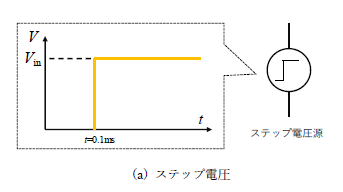
まずは受動素子の両端に図4(a)の電圧を印加します。これは図 4(a)に示す通り、電圧がt =0.1ms で 0→ V inに変化する電圧源です。パ ワエレではステップ上に電圧が受動素子に印加されることが多いので、この電圧源とともに受動素子の電圧と電流の変化を追っていきましょう。
それではまず抵抗です。
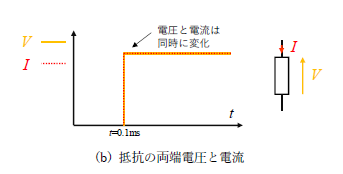
図 4(b)の通り、抵抗にステップ状の電圧を印加した場合、その両端の電圧と抵抗に流れる電流はどのようになるでしょうか?図を確認すると、オームの法則V=IRから電圧が印加されると同時に電流が流れており、その波形はそれぞれ同じ形になることが確認できます。つまり、純粋な抵抗の電圧と電流波形は同じ形となるのです。
もし皆さまが抵抗の両端電圧と流れる電流を実際に測定して、波形が異なった場合、それは純粋な抵抗ではなく、何か他の素子の影響が見えていることとなります。これが結構重要で、抵抗がおかしいのか測定器がおかしいのかの判断材料にもなります。
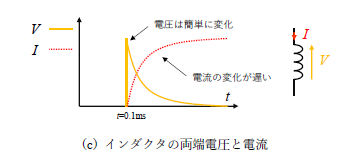
続いて、インダクタです。インダクタにステップ状の電圧をt =0.1ms で印加した場合、インダクタの両端電圧は簡単に変化していますが、インダクタは電流の変化を嫌うのでその大きさは徐々に増加してきます。これは電流の変化を嫌うインダクタの特性を考えると納得できますよね。
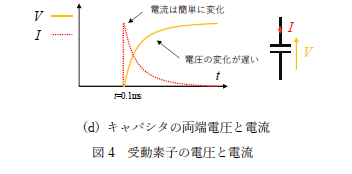
最後にキャパシタです。キャパシタにステップ状の電圧をt =0.1ms で印加した場合、キャパシタ電流はすぐに変化できますが、電圧の変化を嫌うので、その大きさは徐々に増加してきます。これも電圧の変化を嫌うキャパシタの特性を考えると納得できますよね。
よくわからないので、数式が欲しいあなたには交流理論で考えてみましょう。インダクタのインピー ダンスの大きさは ωL、キャパシタのインピーダンス の大きさは 1/ωC で表現できます。ここで ω=2πf で f は交流電圧や交流電流の周波数です。このインダクタ は電源電圧変化時(高周波成分を多く含む)にインピーダンスが大きく、キャパシタは電源電圧変化時(高周波成分を多く含む)にインピーダンスが小さくなることが予測できます。この考え方からもインダクタの電圧波形は変化時が最も大きく、キャパシタの電流波形も変化時が最も大きいと理解できるでしょう。ではt =∞ではどうなるのでしょうか? t =∞では周波数はほぼ 0 なので、インダクタのインピーダンスの大きさは 0 となり、その両端電圧は 0、キャパシタのインピーダンスの大きさは∞となり、両端電圧はV inになります。
皆さんおわかりいただけましたでしょうか?本日はここまで。お読みいただきありがとうございます。
参考・引用文献
[1] いらすとや HP.
[2] freepic.






 :
: :
: